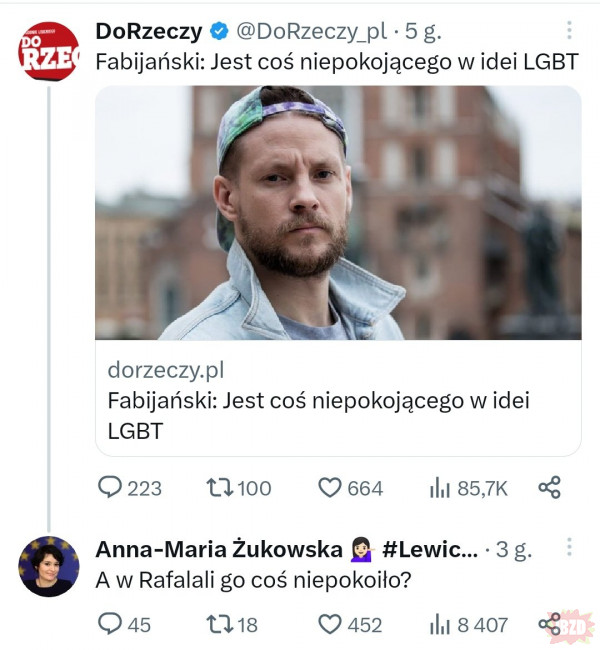
Kiedy jesteś tak żałosny że najpierw wyruchał Cię trans a potem zaorała nawet Żukowska
Humor
1 r
13